7月17号出发来北京,买了8月17号的票回上海,整整在北京待了一个月。马上就要开学了,CSRC 暑研也暂时告一段落,在此总结一下我在北京的工作。
工作背景
来到中心的第一天,徐老师跟我简单聊了聊组里的工作,展示了一些工作成果,给了我一个开放性的研究题目( 他的一个博士后正在做 ),还有一本 Steven H. Strogatz 的《 Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering 》,让我自己先看一看。我的工作主要涉及到了这本书里的 fixed point 和 bifurcation 等概念:
- In an \(n\)-dimensional phase space with coordiantes \((x_1, \dots,x_n)\), we introduced the general system:
and its solutions could be visualized as trajectories.
-
The simplest case \(n=1\) one-dimensional system, namely \(\dot{x}=f(x)\). Plot \(\dot{x}\) versus \(x\), and draw arrows on the \(x\)-axis to indicate the corresponding velocity vector at each \(x\): for \(\dot{x}>0\), \(\rightarrow\); for \(\dot{x}<0\), \(\leftarrow\). At points where \(\dot{x}=0\), there is no flow; such points are called fixed points.
-
Assuming the fixed points of \(\dot{x}=f(x)\) is \(x^*\): \(f'(x^*)<0 \Rightarrow x^*\) is a stable fixed point; \(f'(x^x)>0 \Rightarrow x^*\) is an unstable fixed point.
-
bifurcation: the qualitative structure of flow (vector fields) can chages as parameters are varied, and fixed points can be created or destroyed, or their stability can change. These qualitative changes in the dynamics are called bifurcation.
工作开始
我在北京的工作围绕着一篇文献展开 Geometric capture and escape of a microswimmer colliding with an obstacle,这篇文献主要模拟了当 microswimmer 在流体中和一个固定的球形 obstacle 碰撞会产生的 geometric capture 和 escape 现象。
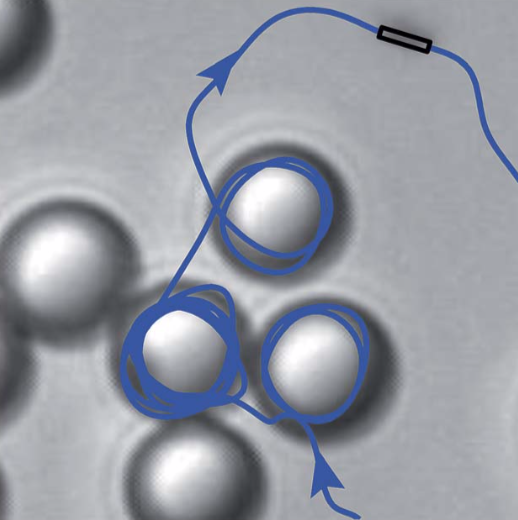
▲ Snapshots from the experiments of Takagi et al.
在实验中已经观察到这个现象,Takagi et al 实验给出图中就可以看到一个 self-propelled body 在 colloid-filled bath 中运动时,有时会一直绕着球体circling,有时又会随机逃逸出绕球运动的轨道。对于这个固定球体来说,即存在一个临界半径,当半径大于这个 critical 半径 \(A_c\) 时,swimmer就会一直绕着球体运动。
分析研究
为了分析这个现象,我们要考虑 microswimmer 在流体中的运动方程,它的速度由两部分组成,一个是 swimmer 自身的驱动速度 \(\mathbf{e}\) , 另一部分即流场的速度 \(\mathbf{u}\) , 故 microswimmer 的速度可以写成 \(\frac{\mathrm{d}\mathbf{x}_0}{\mathrm{d}t}=\mathbf{e}+\mathbf{u}\) ,其中 \(\mathbf{e}\) 的方向由 Faxén’s Law 确定: \(\frac{\mathrm{d}\mathbf{e}}{\mathrm{d}t}=\mathbf{\Omega}\times\mathbf{e}\) 。
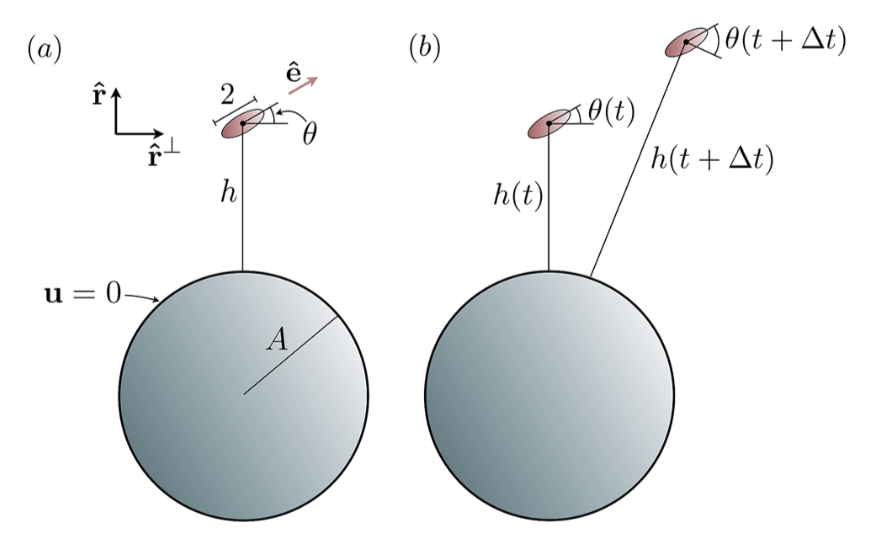
▲ Illustration of the colloid/swimmer system
根据上图可将其改写成 \(h\) 和 \(\theta\) 的方程,便可以得到 \(\frac{\mathrm{d}h}{\mathrm{d}t}\) 和 \(\frac{\mathrm{d}\theta}{\mathrm{d}t}\) 的表达式,由此画出 \(h-\theta\) 相图以寻找 fixed points.
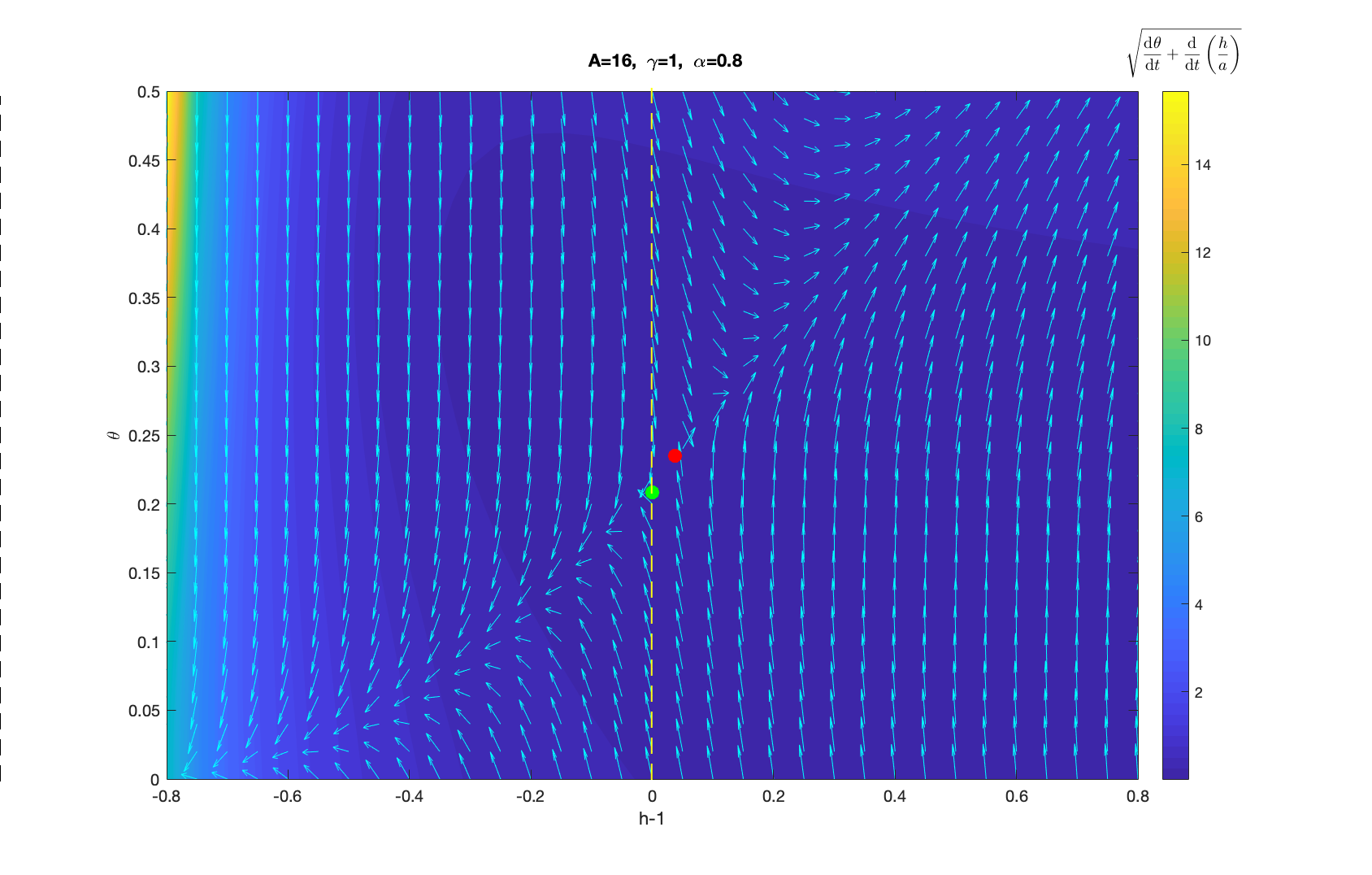
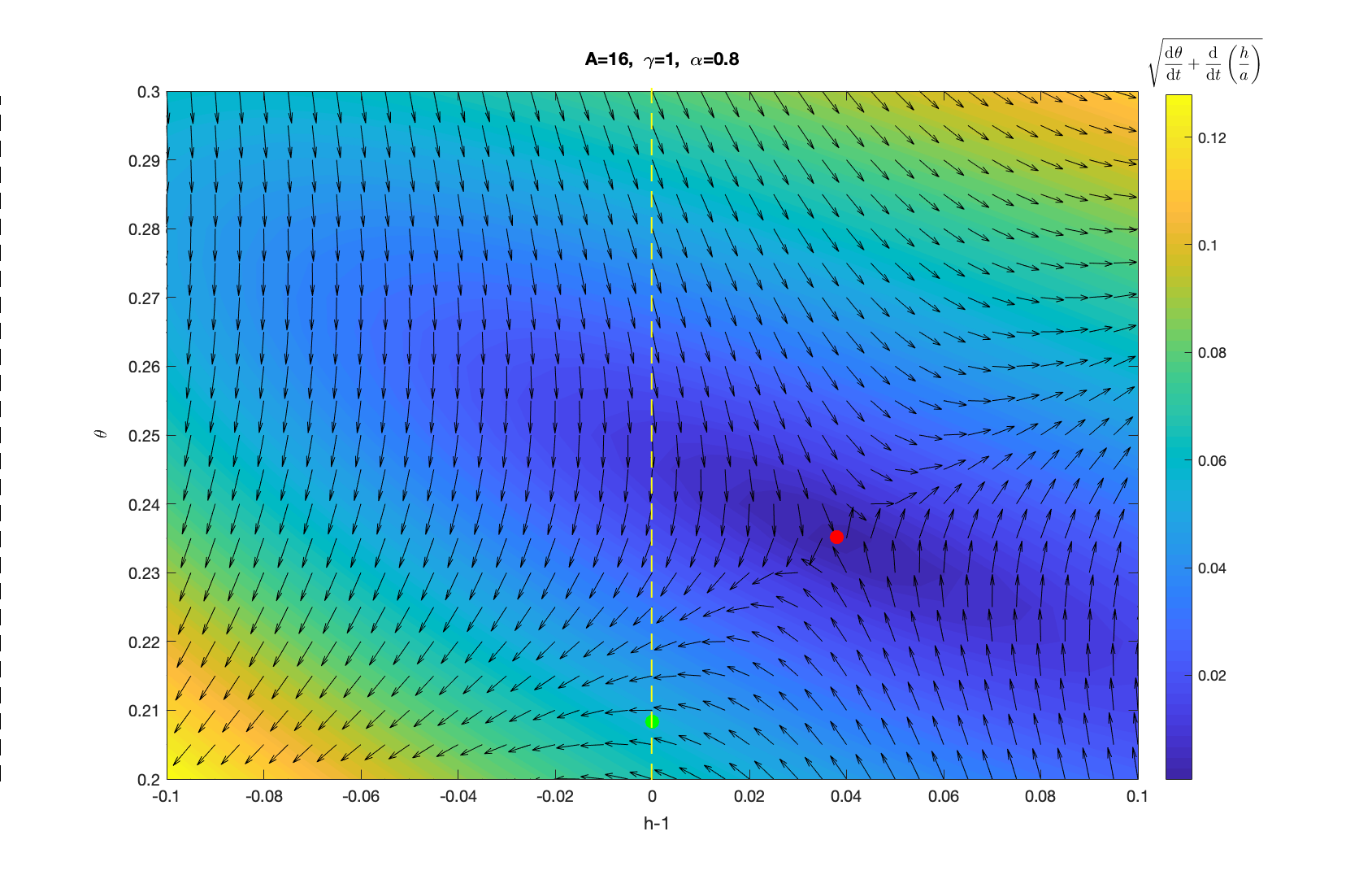
▲ \(A=16, \gamma=1, \alpha=0.8\) 时的 \(h-\theta\) 相图 ▲ 放大后 \(h=1\) 附近的 \(h-\theta\) 相图
从图中可以看到红色点是解出来的 fixed point 所在,但不幸的是,它并不是一个稳定的 fixed point ,只要有一点微扰,他就会偏向其他 \(h\) 和 \(\theta\), 但是如果我们取 swimmer 的半径为1,仅考虑 \(h\geqslant1\) 时的情况,就可以发现在绿点所在位置存在一个 fixed point。如果仅保留一阶小量可以推出存在临界半径
\[A_c=\frac{128\bar{h}^5}{9\alpha^2(2-\it{\Gamma})}.\]通过数值计算模拟 swimmer 在流体中的 trajectories, 确实可以得到绕球和不绕球两种运动轨迹 ( GIF 文件较大,且国内网络 GitHub 加载较慢,请耐心等候):
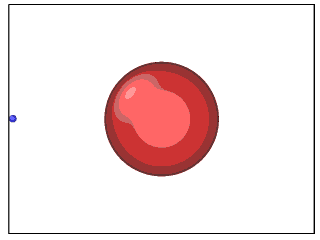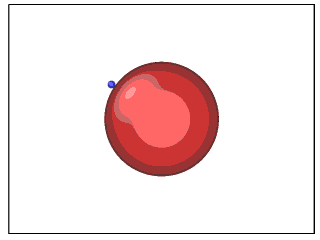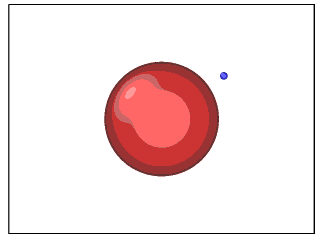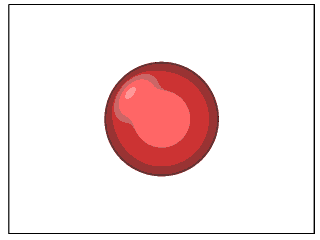
▲ \(A=15, \gamma=1, \alpha=0.8\) 时的运动轨迹 ▲ \(A=20, \gamma=1, \alpha=0.8\) 时的运动轨迹
工作结果
利用CSRC的高性能服务器我们可以进行大量数据的计算,在这里展示部分计算结果:
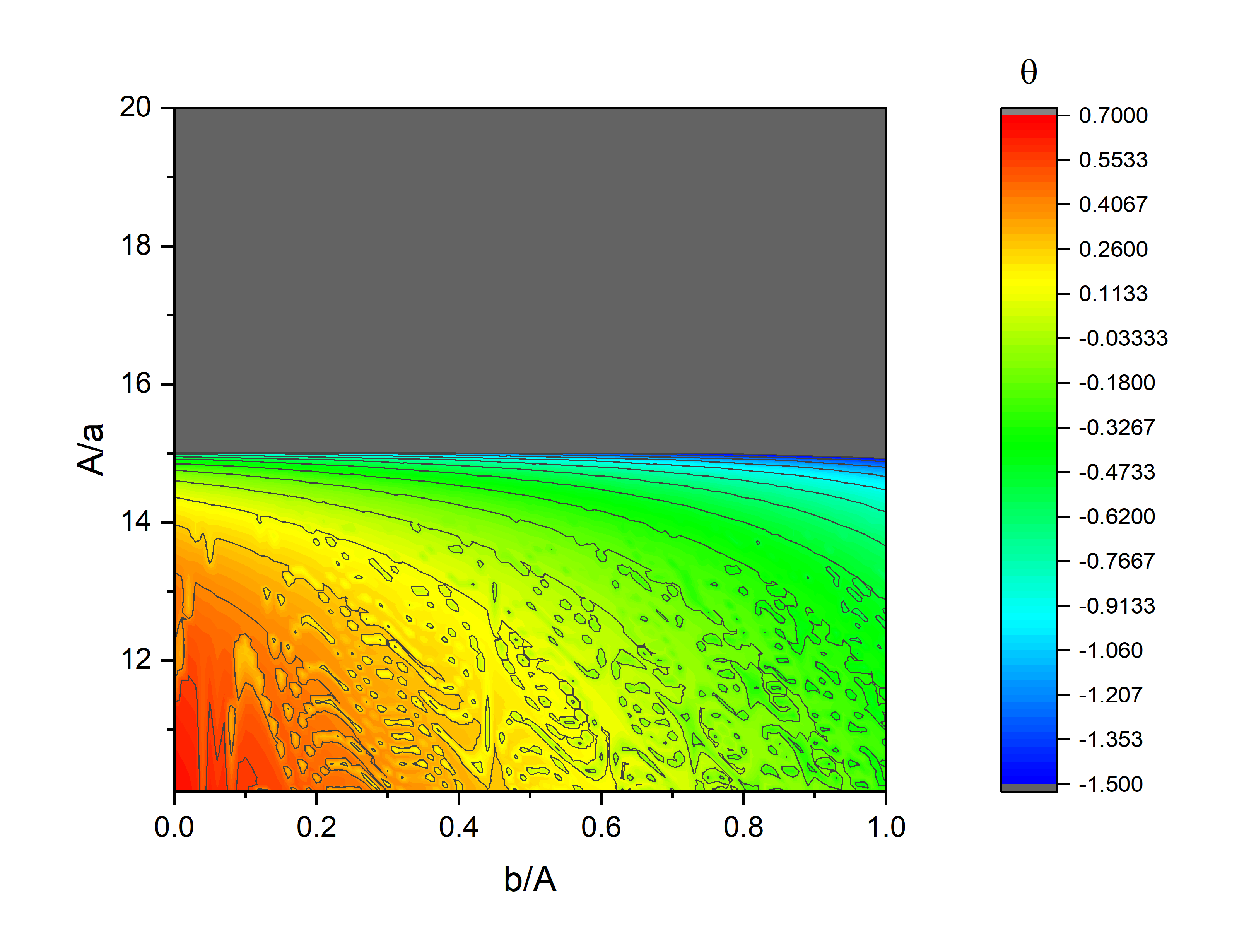
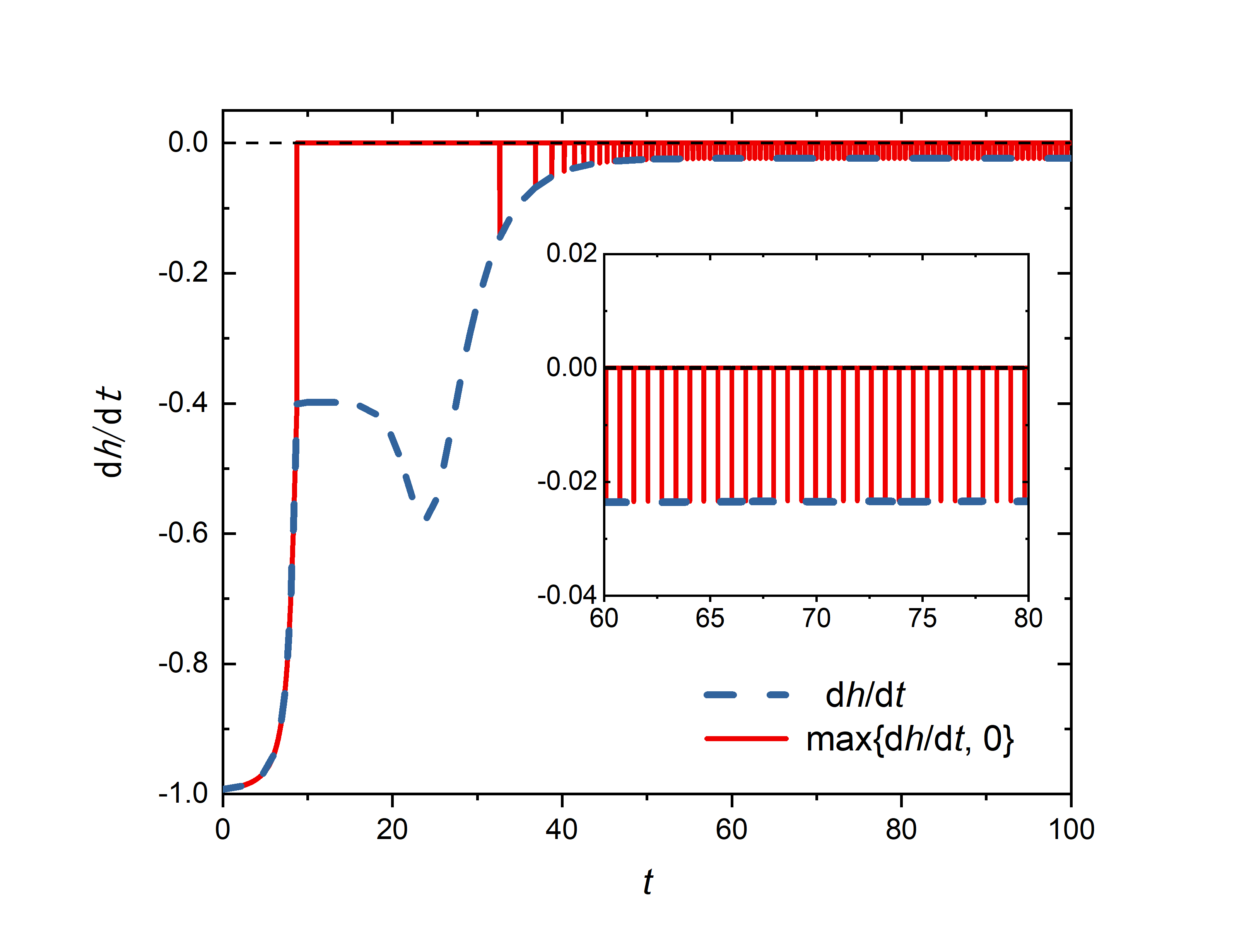
▲ 不同 \(A\) 和入射纵坐标 \(b\) 对出射角 \(\theta\) 的影响 ▲ 径向速度 \(\mathrm{d}h/\mathrm{d}t\) 理论和实际值的差别
最后画出 microswimmer 整个运动过程中 \(h-\theta\) 随时间的变化 ( GIF 文件较大,且国内网络 GitHub 加载较慢,请耐心等候):
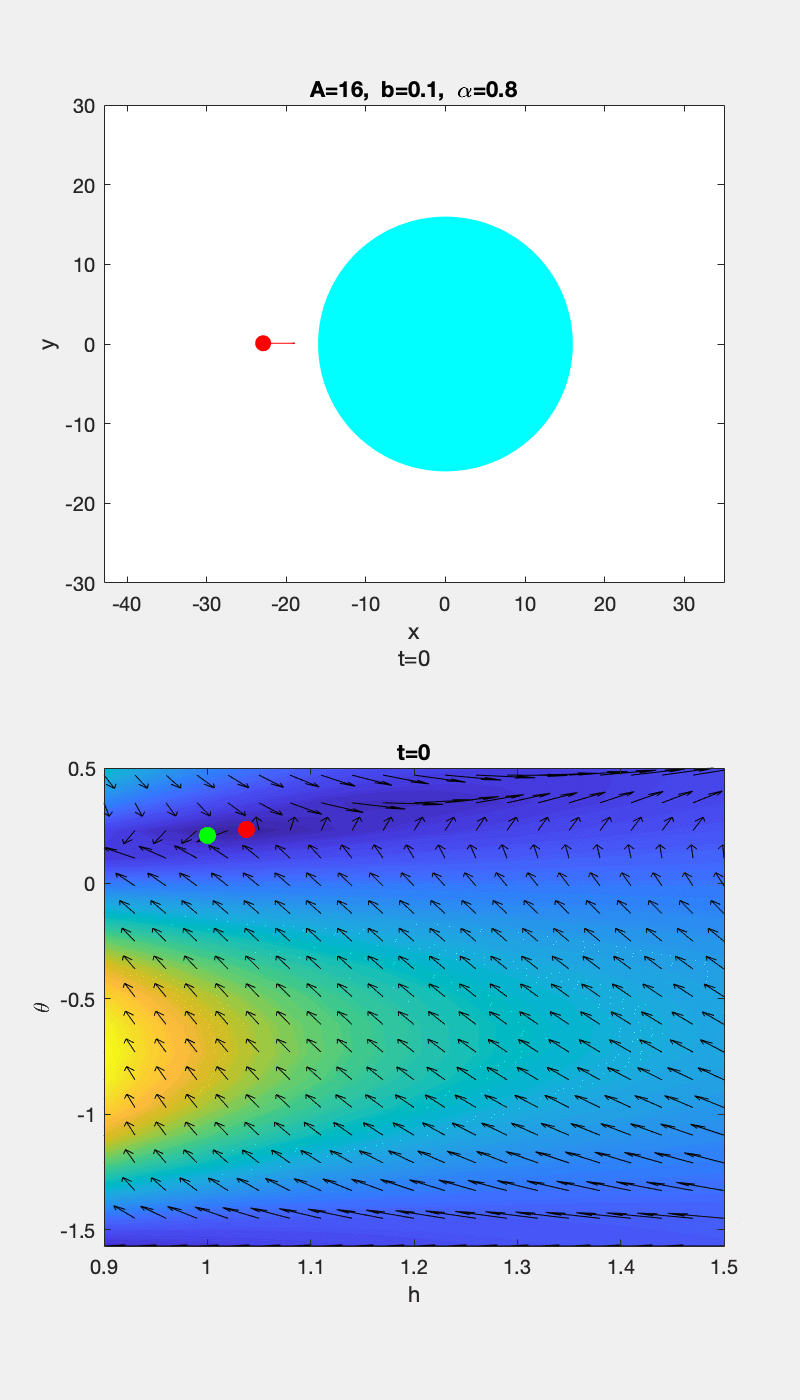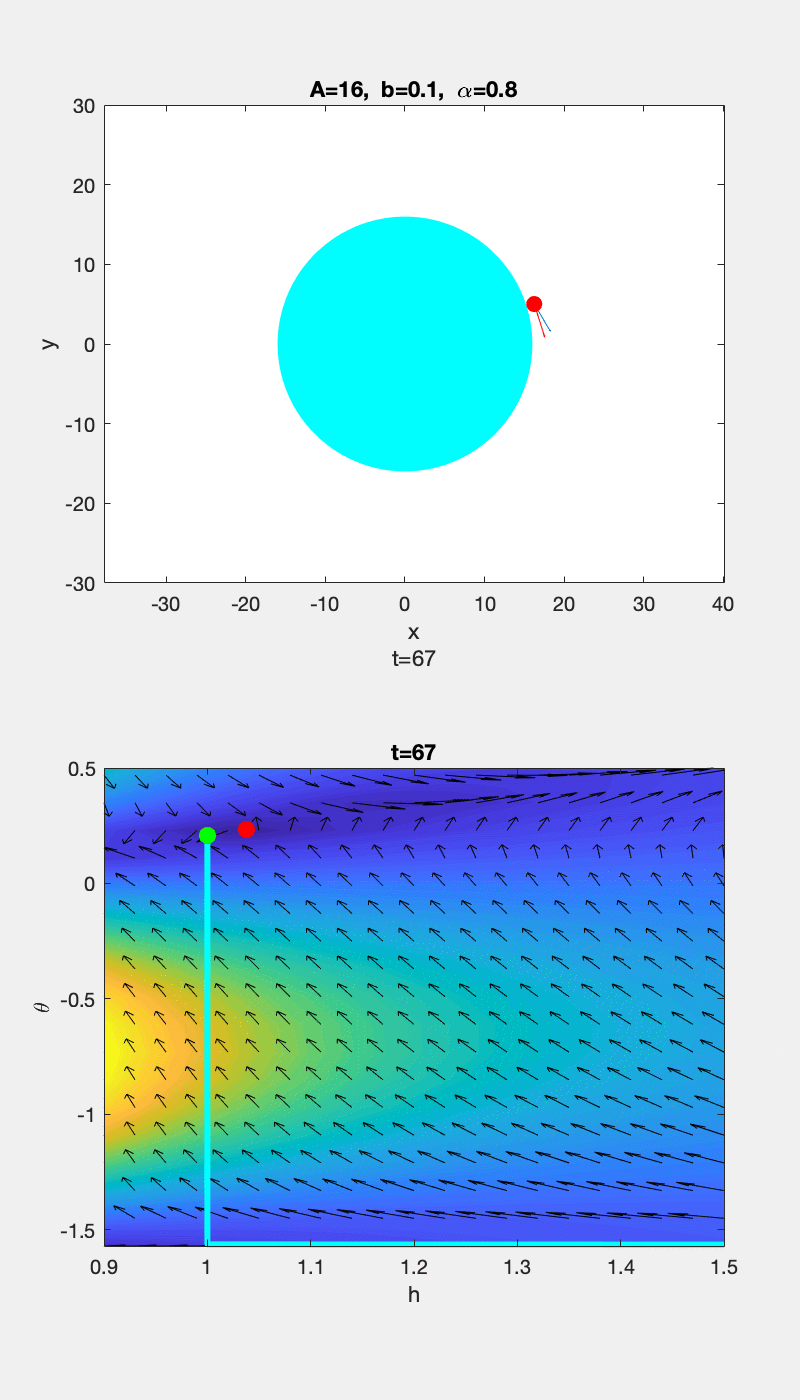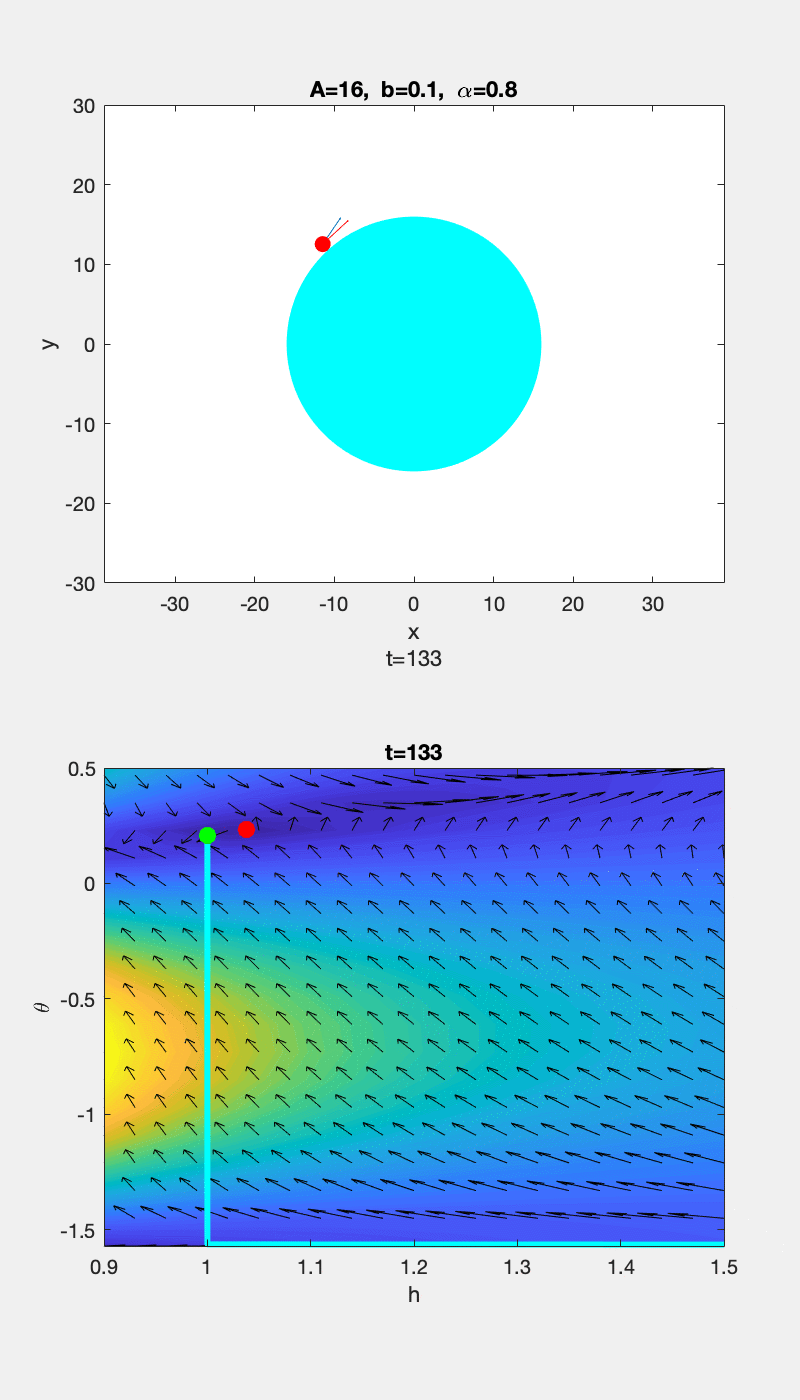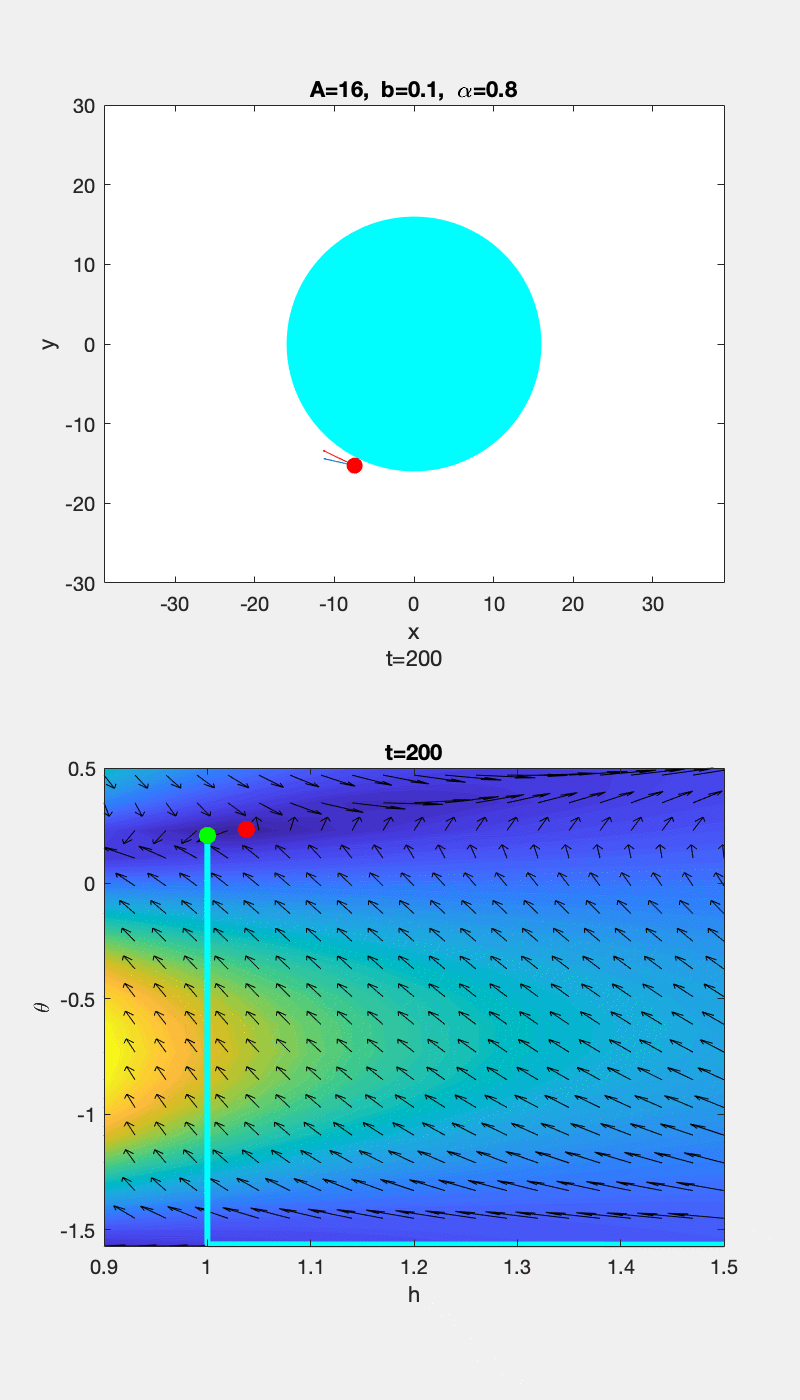
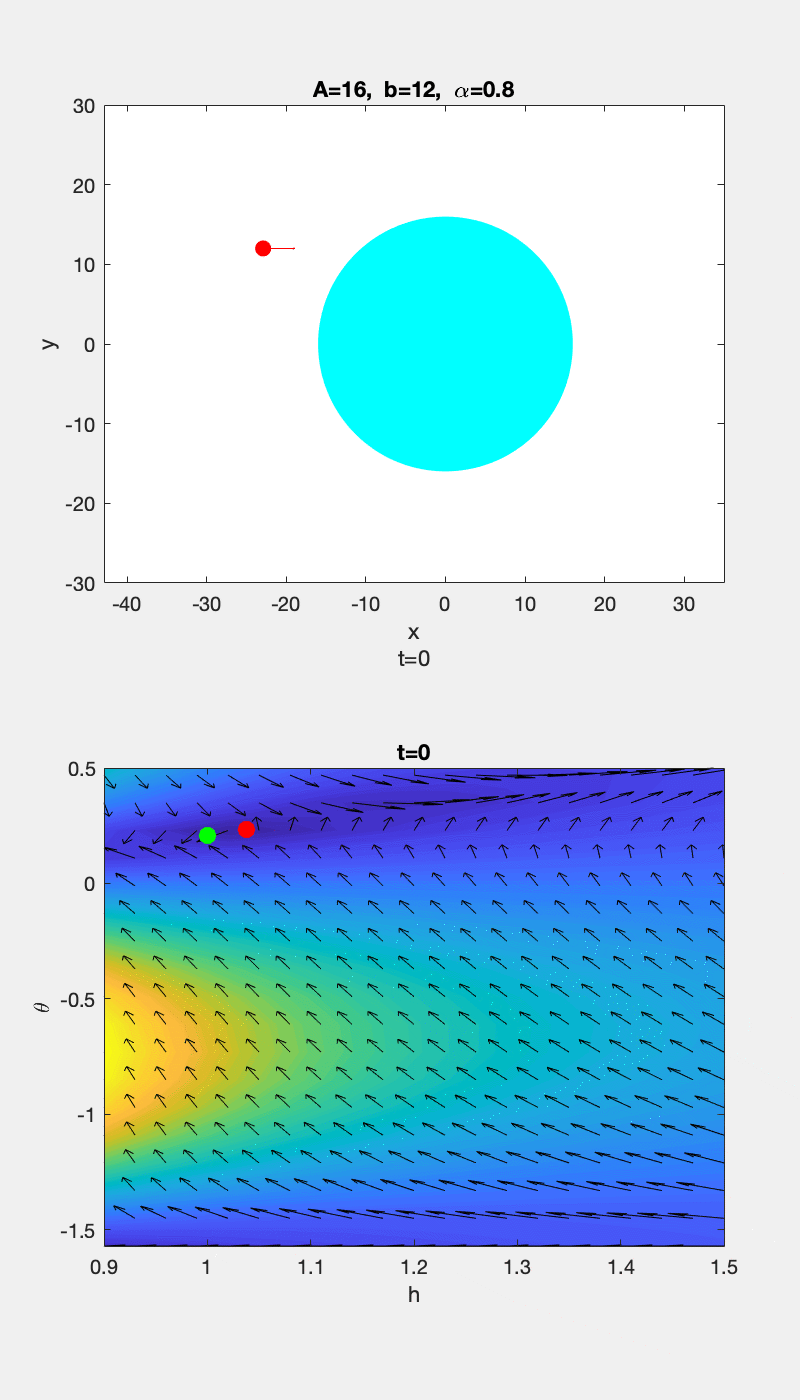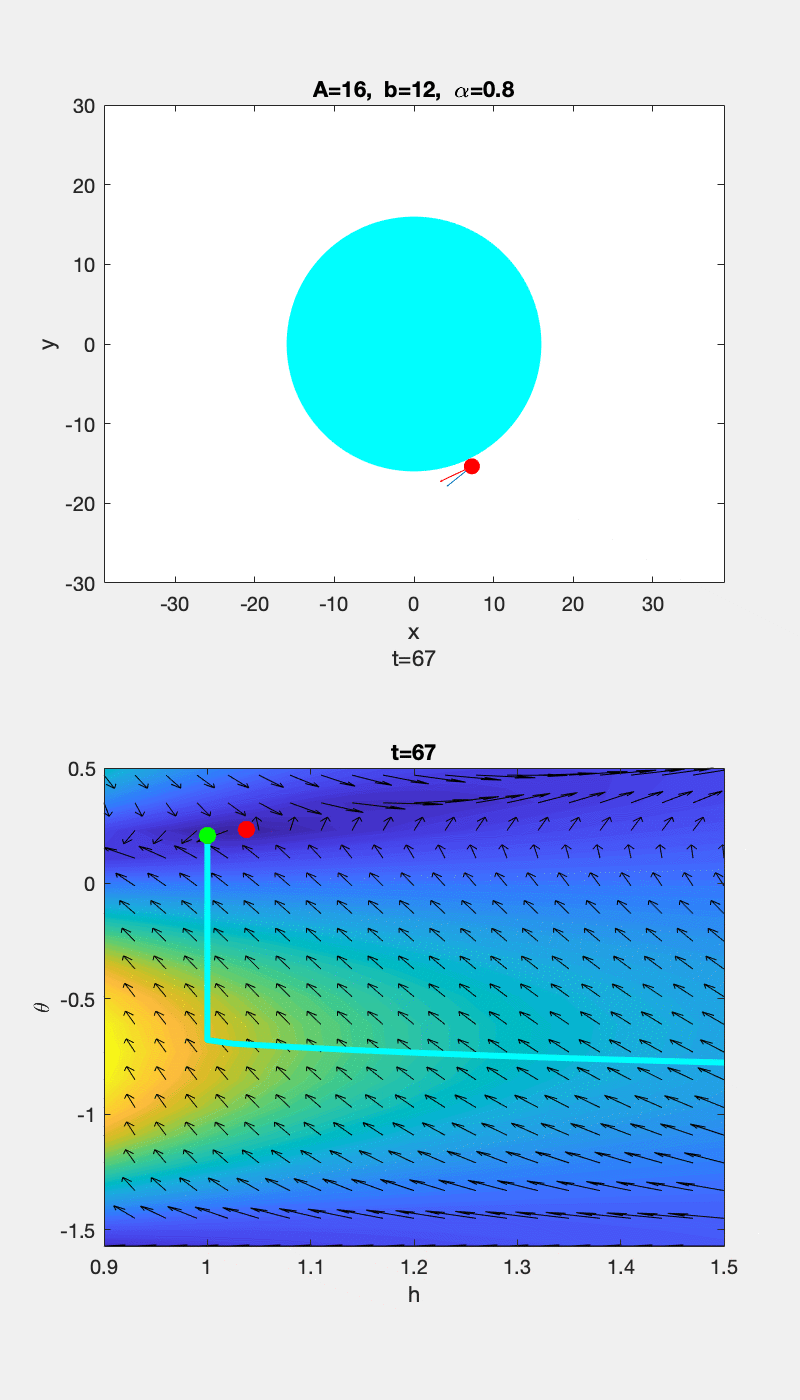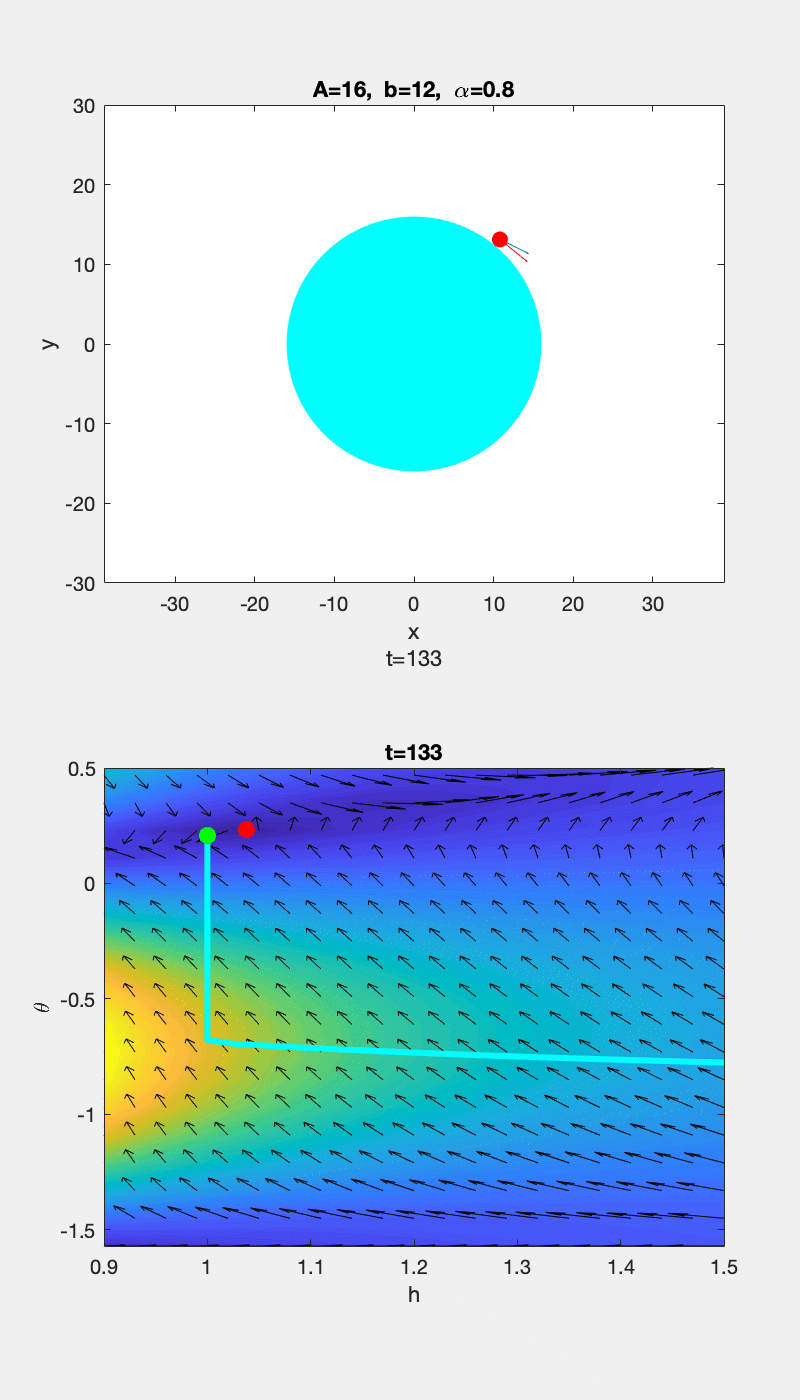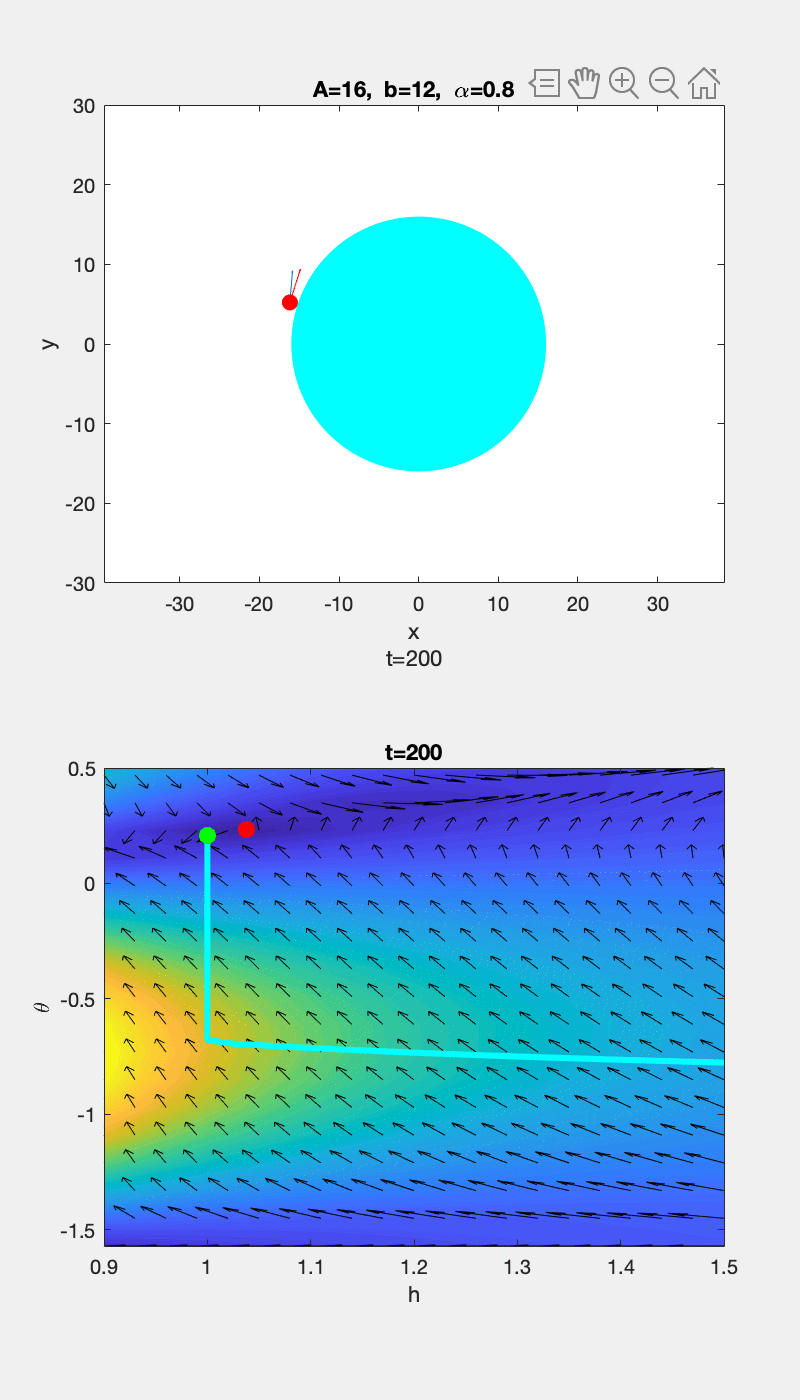
▲ \(b=0.1\) 时运动轨迹和 \(h-\theta\) 随时间的变化情况 ▲ \(b=12\) 时运动轨迹和 \(h-\theta\) 随时间的变化情况
为了更清楚的显示趋势,上图中的 vector 在 \(\theta\) 方向的分量被放大了,所以 \(h-\theta\) 曲线的切线方向和 vector 的方向没有重合。下面给出没有 scale 前的图,并用红色箭头标出切线方向,可以看到曲线的切线方向和 vector 方向的确是重合的:
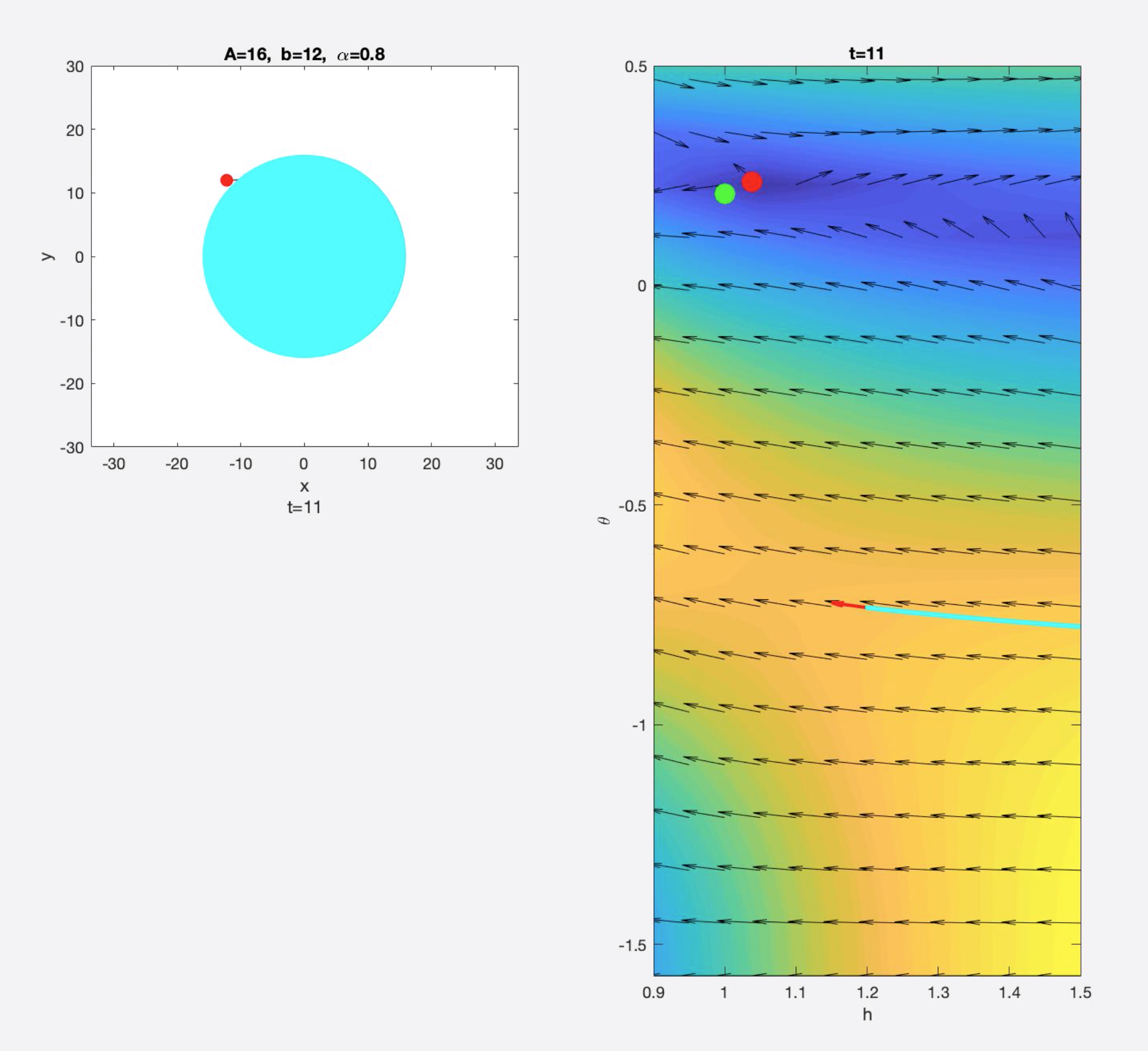
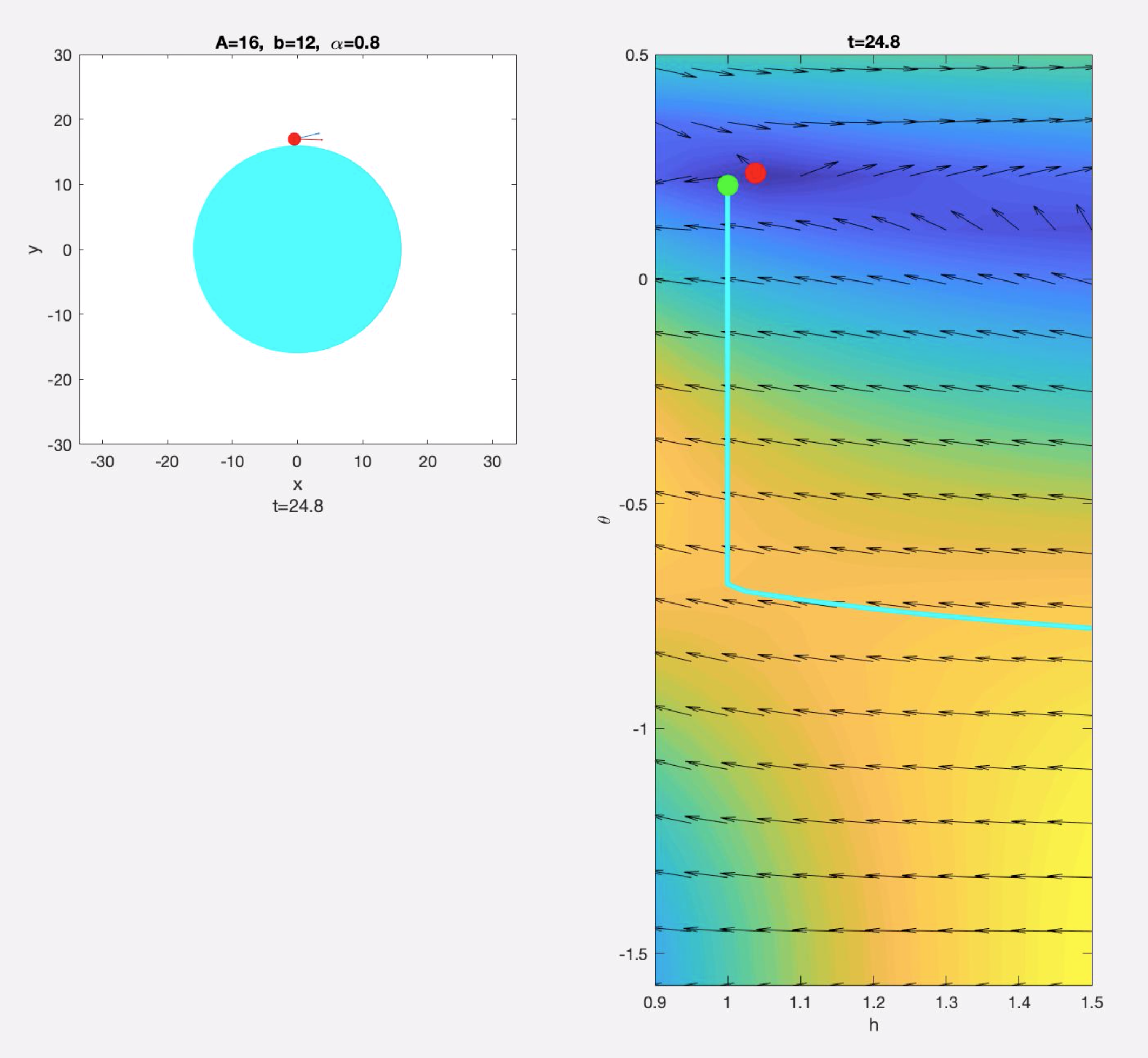
▲ \(t=11\) 时运动轨迹和 \(h-\theta\) 的变化情况 ▲ \(t=24.8\) 时运动轨迹和 \(h-\theta\) 的变化情况
综上分析可知 swimmer 会出现绕球运动是因为绿色的 fixed point 的存在,并不是因为求解得到的那个红色的不稳定 fixed point ,由此可以看出这篇文章其实写得有些问题。。。
附录
因为一开始博士后师兄给了我他的 Matlab 代码作为参考,未经他允许公开他的代码不太好,所以仅在这附上我自己写的 C++ 代码。
/*
*
* Created by WW on 2019-8-8.
* Copyright © WW. All rights reserved.
*
*/
#include <iostream>
#include <time.h>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <fstream>
#include <string.h>
#include <unistd.h>
#include <sys/stat.h>
#define NSPHR 2
#define NDIM 2
#define NSTEP 1e5
#define dt 1e-3
#define NR_END 1
using namespace std;
//============================================================================================
void nrerror(const char error_text[])
/* Numerical Recipes standard error handler */
{
fprintf(stderr,"Numerical Recipes run-time error...\n");
fprintf(stderr,"%s\n",error_text);
fprintf(stderr,"...now exiting to system...\n");
exit(1);
}
double *dvector(long nl, long nh)
/* allocate a double vector with subscript range v[nl..nh] */
{
double *v;
v = (double *)malloc((size_t) ((nh-nl+1+NR_END)*sizeof(double)));
const char *a = "allocation failure in vector()";
if (!v) nrerror(a);
return v-nl+NR_END;
}
//============================================================================================
void procBar(int rate)
//进度条
{
int ratep = rate/2;
char bar[52];
const char *label = "|/-\\";
memset(bar, 0, 52*sizeof(char));
int i = 0;
while(i <= ratep)
{
bar[i] = '=';
i++;
}
fflush(stdout);
printf("Proc:[%-51s][%d%%][%c]\r", bar, rate, label[rate%4]);
}
//============================================================================================
double Gamma(double gam)
{
return (1-(gam*gam))/(1+(gam*gam));
}
double Q(double Rtra, double rh, double theta)
{
return (pow(Rtra, 6))-5*(pow(Rtra, 4))*((Rtra+rh)\
*(Rtra+rh))+10*(Rtra*Rtra)*(pow((Rtra+rh), 4))\
+6*(pow((Rtra+rh), 6))+(9*(pow(Rtra, 6))-29*(pow(Rtra, 4))*(pow((Rtra+rh), 2))\
+34*(pow(Rtra, 2))*(pow((Rtra+rh), 4))-18*(pow((Rtra+rh), 6)))*cos(2*theta);
}
//============================================================================================
int main(int argc, char **argv)
{
time_t start,end;
start=time(NULL); //简单计时
cout<<"Running..."<<endl<<endl;
int num;
sscanf(argv[1], "%d", &num);
//============================================================================================
char path[10];
sprintf(path,"./data");
if(access(path,0) == -1)
{
printf("%s is set up./n", path);
mkdir(path,0777);
}
char Contour[30];
sprintf(Contour, "%s/Contour%d.txt", path, num);
FILE *file2;
file2 = fopen(Contour, "a+");
//==============================================
double Rtra;
double Rx, Ry, ratio;
//for(int i = 0; i <= 50; i ++)
{
//Rtra = 15+i*0.1;
Rtra = 15+num*0.1;
//for(int j = 0; j <= 100; j++)
{
//ratio = 0.00+j*0.005;
ratio = 0.01;
Ry = Rtra*ratio;
double Rhead = 1.0;
double Alpha = 0.8;
double gam = 1.0;
cout<<"A: "<<Rtra<<"\t Alpha: "<<Alpha<<"\t gamma: "<<gam<<"\tRy0: "<<Ry<<endl;
//==============================================
Rx = -25;
double *X0; //bacterium position
X0 = dvector(1, NDIM);
X0[1] = Rx;
X0[2] = Ry;
double rh = sqrt(Rx*Rx+Ry*Ry);
double *r1, *r2 , *e, *ep, *V;
r1 = dvector(1, NDIM);
r1[1] = Rx/rh;
r1[2] = Ry/rh;
r2 = dvector(1, NDIM);
r2[1] = r1[2];
r2[2] = -r1[1];
double th, theta;
th = atan2(r2[2], r2[1]);
e = dvector(1, NDIM);
ep = dvector(1, NDIM);
V = dvector(1, NDIM);
e[1] = 1.0;
e[2] = 0.0;
//============================================================================================
char Trajectory[100];
sprintf(Trajectory, "%s/TraR-Rhead=%.2f-Rtra=%.2f-b=%g.lammpstrj", path, Rhead, Rtra, Ry);
FILE *file;
file = fopen(Trajectory, "w");
//============================================================================================
char filename[100];
sprintf(filename, "h_theta-Rhead=%.2f-Rtra=%.2f-b=%g.txt", Rhead, Rtra, Rtra*ratio);
//ofstream fout("%s/dh_dt-Rhead=%.2f-Rtra=%.2f-b=%g.txt");
ofstream fout2(filename);
//==================================================
int counter = 0;
double dhmax = -10;
for(int t = 1; t <= NSTEP; t++)
{
rh = sqrt(Rx*Rx+Ry*Ry);
r1[1] = Rx/rh;
r1[2] = Ry/rh;
r2[1] = r1[2];
r2[2] = -r1[1];
th = atan2(r2[2], r2[1]);
ep[1] = cos(th)*e[1] + sin(th)*e[2];
ep[2] = -sin(th)*e[1] + cos(th)*e[2];
theta = atan2(ep[2], ep[1]);
double T = t*dt;
rh = rh-Rtra;
fout2<<T<<"\t"<<rh<<"\t"<<theta<<endl;
//==============================================
if(rh <= Rhead+0.2 && counter == 0)
{
counter++;
}
if(rh > 5 && counter == 1)
{
counter++;
//fprintf(file2, "%lf\t%lf\t%lf\t%lf\n", ratio*Rtra, ratio, Rtra, atan2(V[2], V[1]));
break;
}
//==============================================
double u1, u2;
u1 = (-3*Rtra*Alpha*(1-3*(sin(theta)*sin(theta)))*(Rtra+rh))/\
(2*(rh*rh)*((2*Rtra+rh)*(2*Rtra+rh)));
u2 = (3*(Rtra*Rtra*Rtra)*Alpha*(2*(Rtra*Rtra)\
+6*Rtra*rh+3*(rh*rh))*sin(2*theta))/\
(4*(rh*rh)*((Rtra+rh)*(Rtra+rh)*(Rtra+rh))*((2*Rtra+rh)*(2*Rtra+rh)));
double Omega;
Omega = (-3*Alpha*(Rtra*Rtra*Rtra)*sin(2*theta))/\
(4*(rh*rh*rh)*((Rtra+rh)*(Rtra+rh))*((2*Rtra+rh)*(2*Rtra+rh)*(2*Rtra+rh)))\
*((2*(Rtra*Rtra)+6*Rtra*rh+3*(rh*rh))+(Gamma(gam)*Q(Rtra, rh, theta))/\
(8*(Rtra*Rtra)*((Rtra+rh)*(Rtra+rh))));
th = atan2(e[2], e[1]);
e[1] = cos(th+Omega*dt);
e[2] = sin(th+Omega*dt);
V[1] = u1*r1[1]+u2*r2[1]+e[1];
V[2] = u1*r1[2]+u2*r2[2]+e[2];
// print dh/dt
//fout<<T<<"\t"<<(V[1]*r1[1]+V[2]*r1[2])<<"\t";
if((V[1]*r1[1]+V[2]*r1[2]) > dhmax)
dhmax = (V[1]*r1[1]+V[2]*r1[2]);
double dh, phi, omega;
dh = V[1]*r1[1]+V[2]*r1[2];
phi = atan2(r1[2], r1[1]);
omega = (V[1]*r2[1]+V[2]*r2[2])/(rh+Rtra);
// dh/dt>0 when rh=Rhead
if(rh <= Rhead && dh < 0.0)
{
dh = 0.0;
}
rh = rh+dh*dt;
phi = phi-omega*dt;
//fout<<(V[1]*r1[1]+V[2]*r1[2])<<endl;
Rx = (rh+Rtra)*cos(phi);
Ry = (rh+Rtra)*sin(phi);
X0[1] = Rx;
X0[2] = Ry;
//============================================================================================
if(t%100 == 0)
{
fprintf(file, "ITEM: TIMESTEP\n");
fprintf(file, "%d\n", t);
fprintf(file, "ITEM: NUMBER OF ATOMS\n");
fprintf(file, "%d\n", NSPHR);
fprintf(file, "ITEM: BOX BOUNDS pp pp pp\n");
fprintf(file, "-40 40\n");
fprintf(file, "-30 30\n");
fprintf(file, "-0.5 0.5\n");
fprintf(file, "ITEM: ATOMS id type x y z Radius\n");
fprintf(file, "1 1 %f %f 0 %f\n", 0.0, 0.0, Rtra);
fprintf(file, "2 2 %f %f 0 %f\n", Rx, Ry, Rhead);
}
procBar(t*100/NSTEP);
}
cout<<endl;
//fout.close();
fout2.close();
fclose(file);
//======================================================
if(counter == 1)
{
cout<<"circling"<<endl;
fprintf(file2, "%lf\t%lf\t%lf\t%lf\n", ratio*Rtra, ratio, Rtra, dhmax);
//fprintf(file2, "%lf\t%lf\t%lf\t%lf\n", ratio*Rtra, ratio, Rtra, -10.0);
}
if(counter == 2)
cout<<"escape"<<endl;
cout<<endl;
//======================================================
}
}
fclose(file2);
//============================================================================================
//计时结束并输出所用时间
end=time(NULL);
cout<<"程序结束!"<<endl;
int T,second,minute,hour;
T=end-start;
second=T%60;
minute=T/60;
hour=minute/60;
minute=minute%60;
cout<<"用时:"<<hour<<" h "<<minute<<" min "<<second<<" s.\n";
return 0;
}

